문제 링크
https://programmers.co.kr/learn/courses/30/lessons/12979
코딩테스트 연습 - 기지국 설치
N개의 아파트가 일렬로 쭉 늘어서 있습니다. 이 중에서 일부 아파트 옥상에는 4g 기지국이 설치되어 있습니다. 기술이 발전해 5g 수요가 높아져 4g 기지국을 5g 기지국으로 바꾸려 합니다. 그런데 5
programmers.co.kr
풀이
전체적인 풀이 과정은 다음과 같다.
- 기존 기지국의 범위 외의 구역을 구간으로 가정해 구분 (구간 시작 ~ 첫 번째 기지국, 기지국 사이의 구간, 마지막 기지국 ~ 구간 끝 구간)
- 해당 구간을 하나의 기지국 범위 (2 * w + 1) 로 나누어 올림 적용하여 누적 합 계산
문제의 접근 방식을 다르게 생각해야 하는 문제이다. 문제의 첫 인상으로는 마치 일차원의 배열에 기존 기지국들의 위치와 커버 범위에 값을 설정하고, 이후 처음부터 반복문으로 비어 있는 곳들의 값을 바꾸며 추가 기지국들의 개수를 더해야 하는 것으로 보인다. 하지만 그렇게 배열 요소를 반복문으로 모두 탐색하려 하는 경우 조건 상 배열의 최대 길이가 2억이기 때문에, 시간 초과가 발생할 수 있으므로 불가능하다.
그렇다면 요소 하나하나를 접근하는 것보다, 구간 단위로 접근하면 훨씬 빠르게 계산이 가능하다.
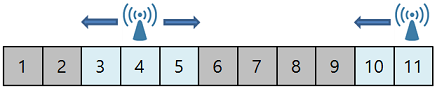
예시 속 사진 처럼 양 끝과 기지국, 기지국과 기지국 사이의 빈 구간 길이를 계산하고, 구해진 구간 길이를 한 기지국의 커버 범위로 나눈다음 올림 처리를 하면, 하나의 구간을 커버 가능한 기지국의 개수가 구해진다. 이를 구할 수 있는 모든 구간에 적용한 다음 답을 누적하기만 한다면 쉽게 답을 구할 수 있다.
class Solution {
public int solution(int n, int[] stations, int w) {
int answer = 0, sectionLength;
for (int i = 0; i <= stations.length; i++) {
if(i == 0){//구간 시작부터 ~ 첫번째 기지국 구간
sectionLength = stations[i] - 1 - w;
} else if (i == stations.length) {//마지막 기지국 ~ 구간 끝 구간
sectionLength = n - stations[i - 1] - w;
} else {//기지국들 사이의 구간
sectionLength = stations[i] - stations[i - 1] - 2 * w - 1;
}
if (sectionLength >= 0) {
answer += sectionLength / (2 * w + 1);
if (sectionLength % (2 * w + 1) != 0) {
++answer;
}
}
}
return answer;
}
}결과
'Algorithm > 코드 풀이' 카테고리의 다른 글
| 프로그래머스: 스티커 모으기 2 [JAVA] (0) | 2022.03.26 |
|---|---|
| 프로그래머스: 스타 수열 [JAVA] (0) | 2022.03.22 |
| 프로그래머스: 공 이동 시뮬레이션 [JAVA] (0) | 2022.03.15 |
| 프로그래머스: 가장 긴 팰린드롬 [JAVA] (0) | 2022.03.15 |
| 프로그래머스: 베스트앨범 [JAVA] (0) | 2022.03.07 |



