문제 설명
https://www.acmicpc.net/problem/1967
1967번: 트리의 지름
파일의 첫 번째 줄은 노드의 개수 n(1 ≤ n ≤ 10,000)이다. 둘째 줄부터 n-1개의 줄에 각 간선에 대한 정보가 들어온다. 간선에 대한 정보는 세 개의 정수로 이루어져 있다. 첫 번째 정수는 간선이 연
www.acmicpc.net
[문제]
트리(tree)는 사이클이 없는 무방향 그래프이다. 트리에서는 어떤 두 노드를 선택해도 둘 사이에 경로가 항상 하나만 존재하게 된다. 트리에서 어떤 두 노드를 선택해서 양쪽으로 쫙 당길 때, 가장 길게 늘어나는 경우가 있을 것이다. 이럴 때 트리의 모든 노드들은 이 두 노드를 지름의 끝 점으로 하는 원 안에 들어가게 된다.

이런 두 노드 사이의 경로의 길이를 트리의 지름이라고 한다. 정확히 정의하자면 트리에 존재하는 모든 경로들 중에서 가장 긴 것의 길이를 말한다.
입력으로 루트가 있는 트리를 가중치가 있는 간선들로 줄 때, 트리의 지름을 구해서 출력하는 프로그램을 작성하시오. 아래와 같은 트리가 주어진다면 트리의 지름은 45가 된다.
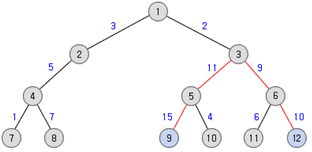
트리의 노드는 1부터 n까지 번호가 매겨져 있다.
[입력]
파일의 첫 번째 줄은 노드의 개수 n(1 ≤ n ≤ 10,000)이다. 둘째 줄부터 n-1개의 줄에 각 간선에 대한 정보가 들어온다. 간선에 대한 정보는 세 개의 정수로 이루어져 있다. 첫 번째 정수는 간선이 연결하는 두 노드 중 부모 노드의 번호를 나타내고, 두 번째 정수는 자식 노드를, 세 번째 정수는 간선의 가중치를 나타낸다. 간선에 대한 정보는 부모 노드의 번호가 작은 것이 먼저 입력되고, 부모 노드의 번호가 같으면 자식 노드의 번호가 작은 것이 먼저 입력된다. 루트 노드의 번호는 항상 1이라고 가정하며, 간선의 가중치는 100보다 크지 않은 양의 정수이다.
[출력]
첫째 줄에 트리의 지름을 출력한다.
[예제 입력 1]
12
1 2 3
1 3 2
2 4 5
3 5 11
3 6 9
4 7 1
4 8 7
5 9 15
5 10 4
6 11 6
6 12 10
[예제 출력 1]
45
풀이
이 문제에서는 단순히 트리의 구조가 주어지는 것 이외에도 그 간선에 대한 가중치 값이 주어지기에, 이들을 모두 저장해야할 필요가 있었다. 게다가 추가적으로 문제에선 단순히 트리라는 언급만 있었기 때문에, 해당 트리 속 특정 노드가 어느 정도로 자식 노드를 가지는 지도 파악이 불가능한 상태이다. 이러한 상태에서 해당 입력들을 저장하기 위해 두개의 벡터 배열을 통해 값을 저장하는 것으로 했다. vector 자료 구조의 push_back() 함수를 활용하면 자식 노드가 다양하더라 도 이들을 순차적으로 값을 넣을 수 있고, size() 함수를 통해선 해당 노드가 자식 유무와 정확한 차수까지도 파악이 가능하기 때문에 이를 사용했다.
지름 계산을 하는 함수로는 재귀함수 기반 DFS로 작성하여, 특정 노드를 중심으로 가장 먼 경로 2개나 1개를 택하여 이를 합하는 것으로 작성했다. 경로 계산을 하는 함수에도 마찬가지로 재귀함수를 기반으로 작성하여 리프 노드까지 함수가 반복된 후 값을 연속되게 반환하는 것으로 작성했다. 그리고 해당 노드에서 지름 계산이 끝난 경우 현재 답과 비교해 답을 교체할 지를 결정하며, 해당 계산이 자식 노드에서도 반복되도록 이를 호출한다.
하지만 이렇게 코드를 작성하고 나니 답은 통과했으나 여타 다른 해답들의 시간과 비교하면 꽤나 오래걸렸는데, 이는 꽤나 많은 재귀함수 호출을 통해 소요되는 시간이 늘어나는 것이다. 그래서 이를 해결하고자 동적 프로그래밍을 사용하여, 각 노드에서 최대 경로 값을 저장하는 배열을 따로 저장하여 이를 지름과 경로 계산에 활용하는 것으로 했다.
#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
vector<int> nodeInfor[10001];//노드 연결 구조 저장
vector<int> linkWeight[10001];//간선 가중치 저장
int cache[10001]; //동적 프로그래밍용
int search(int node) {//재귀함수를 통한 거리 계산
int dist = 0;
if (nodeInfor[node].size() == 0)
return 0;
if (cache[node] != -1)
return cache[node];
for (int i = 0; i < nodeInfor[node].size(); i++) {
dist = max(dist, linkWeight[node][i] + search(nodeInfor[node][i]));
}
return cache[node] = dist;
}
void calDistDFS(int node, int &answer) {//특정 노드를 중심으로 지름 계산
vector<int> distance;
if (nodeInfor[node].size() > 0) {//리프 노드가 아니면
for (int i = 0; i < nodeInfor[node].size(); i++) {
distance.push_back(linkWeight[node][i] + search(nodeInfor[node][i]));
}
sort(distance.begin(), distance.end(), greater<int>());//정렬
if(distance.size() == 1)//자식 노드가 하나만 있으면
answer = max(answer, distance[0]);
else//그 외
answer = max(answer, distance[0] + distance[1]);
}
for (int i = 0; i < nodeInfor[node].size(); i++) {//자식 노드로 내려가 계산 반복
calDistDFS(nodeInfor[node][i], answer);
}
}
int main() {
int n, answer = 0;
cin >> n;
memset(cache, -1, sizeof(cache));
for (int i = 0; i < n - 1; i++) {//입력 저장
int parent, child, weight;
cin >> parent >> child >> weight;
nodeInfor[parent].push_back(child);
linkWeight[parent].push_back(weight);
}
calDistDFS(1, answer);
cout << answer;
return 0;
}결과
아래가 기존 풀이, 위에가 기존 풀이에 동적 프로그래밍을 적용한 경우이다.

'Algorithm > 코드 풀이' 카테고리의 다른 글
| 3584번: 가장 가까운 공통 조상 (0) | 2021.07.04 |
|---|---|
| 1600번: 말이 되고픈 원숭이 (1) | 2021.06.26 |
| 1194번: 달이 차오른다, 가자. (0) | 2021.05.28 |
| 2250번: 트리의 높이와 너비 (0) | 2021.05.28 |
| 1525번: 퍼즐 (0) | 2021.05.19 |



